Logic
Well, for the first time a Norfolk pine has adorned the front page of this Newsletter, and I am sure it is fitting that such a tree be considered the Tree of Logic. From any picture of one, one can see the branches pleasantly grouped, towards the top isolated branches, then a few in pairs, then threesomes and then in larger clusters the lower one gets. And so it is with logic, we add to our concepts, and likewise we must add to our axioms (self evident truths which require no proof).
We do know of course that two frownies make a smiley, as displayed at the top-most point of the Tree of Logic, and of course that it is entirely wishful thinking that two frowns make a smile, but of course two negatives do make an affirmative, when they are ‘composed’.
Now if we try and do an overview of logic, we can either survey how it has developed, or survey its applications. But if you survey its applications, you will view each at its most recent, most technical stage of advance, and you will be looking at matters of similar complexity. Such applications include mathematics, computing, language, the logic of possibility and the logic of time.
If we look at the development of logical theory, Western philosophy sees its beginnings in Classical Greece, and this includes logic, as one of the Classical trivium, which also included grammar and rhetoric. In these Classical times, such pursuits were far from trivial, and rhetoric in particular was essential for the new Athenian ‘democracy’: slavery gave the masters time to be democratic, and logic was a key weapon. Types of fallacy could be collected as an informal analysis, such as argumentum ad hominem, sustaining an argument by attacking the personality of the opponents. But then formalisms appeared, for example in Aristotle’s Prior Analytics the use of symbols for logical variables was used for the first time.
Aristotle further introduced laws such as his Three Basic Laws of Thought, which importantly included the Law of the Excluded Middle. All propositions have to be either true or false. And one of Aristotle’s most detailed systems is that of syllogisms. Maybe we should look a little bit more closely at what syllogisms are about. There are basically three key models, ‘Barbara’ ‘Dimatis/Disamis’ and ‘Daraptis’:
(I, Barbara)
(i) All X is Y,
(ii) All Y is Z,
(iii) Therefore all X is Z.
Note that if we say that no capitalist has a heart, we mean that all capitalists are heartless - or more strictly ‘non-having a heart’. Note also the formulaic convention of using ‘is’ when it will often be replaced by ‘are’. Let us capture Barbara by means of my ‘Bridge of Transitivity’:
Barbara
|
Now modern logicians will say that X need not exist, and if so, Y need not exist, and if the latter, Z need not exist either, so now we can look at our second format, where we change (i):
(II, Dimatis/Disamis)
(i) Some X is Y (Dimatis), or some Y is X (Disamis)
(ii) All Y is Z,
(iii) Therefore some X is Z.
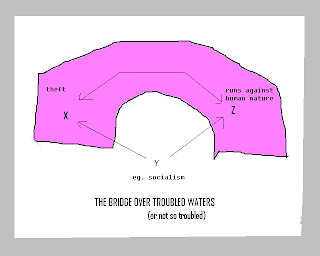
Our third basic form is Daraptis, where we have to assume that ‘all X are Y’ means that X exist, and I give the example from my previous article:
(III, Daraptis)
(i) All socialism (Y) is theft (X),
(ii) All socialism (Y) is against human nature (Z),
(iii) Therefore some theft (X) is against human nature (Z).
Daraptis
|
Now with Laws of Thought, and syllogisms, we have powerful tools in argumentation, be it logic or rhetoric, but when we look at Dimatis and Disamis, they are listed as having the same result, captured in mediaeval mnemonics by having the same vowel pattern, but this doesn’t say why some X are Y means that some Y are X in logical rather than contextual terms.
Developments appear to have lapsed, in the Christian world at least, till around 1100, with the work of Pierre Abélard, born in Brittany in 1079. According to the Stanford Encyclopaedia,
“He is, arguably, the greatest logician of the Middle Ages and is equally famous as the first great nominalist philosopher. He championed the use of reason in matters of faith (he was the first to use ‘theology’ in its modern sense), and his systematic treatment of religious doctrines are as remarkable for their philosophical penetration and subtlety as they are for their audacity.”
Despite Aristotle’s Law of the Excluded Middle, it was Abélard who introduced the doctrine of Limbo, which was accepted by Pope Innocent III. He was later a great icon of the Enlightenment and brought back knowledge of the Classical philosophers to the mediaeval world.
But anything can be examined, and maybe there is an excluded middle, making a similar deduction to Abélard when he deduced there must be a Limbo. Modern logicians say that while the Law of the Excluded Middle is taken as axiomatic, we must be on the safe side, and look to see what coherent systems will look like if we relax this assumption. Those working in Quantum Theory wish to, saying that moving particles can be neither large nor small in their size, despite the logical requirement that a particle must be either small or not small.
So we must perhaps chop off the top of the Tree of Logic:
|
|
But I for one am not sure I’m happy to saw off the branch I am sitting on...
because someone tells me it is to be on the safe side... :][
|
Martin Prior
The Philosophy Takeaway 'Logic' Issue 45